Algebraic Equations list with various kinds of equations that are involved in algebraic equations is discussed below with detailed explanation and examples.
The equation is a mathematical sentence that shows equality of two expressions
Eg: 5+4=9
Simple Equations /Algebraic Equations In Algebraic Equations List
Mathematical equations consisting of at least one variable and an equality sign with two expressions on either side are called simple equations or Algebraic equations.
Eg:
9x=18, 10x-5=25, 6y+4=-5
Equations have expressions on both sides of equal symbol.
The expression which is on the left of the equality sign is the left-hand side (LHS)expression and expression on the right side is called the right-hand side (RHS)expression.
Eg:
10x-5=25
10x-5 is called LHS
25 is RHS.
Depending Upon The Powers Of Variables We Have Different Algebraic Equations In Algebraic Equations List.
| Degree of Equation | Name of the Equation | Representation of Equation |
| 0 | constant | a0 |
| 1 | Linear | a0x+a1 |
| 2 | Quadratic | a0x2+a1x+a2 |
| 3 | Qubic | a0x3+a1x2+a2x+a3 |
| 4 | Biquadratic | a0x4+a1x3+a2x2+a3x+a4 |
Linear Equations In Algebraic Equations List
Algebraic equations with degree 1 are called linear equations.
Linear Equations In One Variable
The linear equations which have only a single variable are linear equations in 1-variable or linear equations with a single variable.
Eg:
4x+3=5, 4x+3=2x+7
Linear Equations In Two Variables
A linear equation which has only two variables in it is called linear equation in 2-variable.
Eg:
x+y=2, 2x+3y=x+5
Any linear equation that can be represented in the form of ax+by+c=0 where a,b and c are real numbers.
Both a and b are not zero generally, represented as a2+b2≠0.
Above examples, can now be represented as
x+y-2=0, x+3y-5=0
Graphical Representation Of Linear Equations In Two Variables For Algebraic Equations In Algebraic Equations List
A linear equation in two variables has an infinite number of solutions.
I,e let us consider a linear equation in 2-variables
x+y=2
put x=0 then y=2
put y=0 then x=2
put x=1 then y=1
put x=3 then y=-1
put y=3 then x=-1
similarly for different values of x we get y value and vice versa.
The solutions of the equation are (0,2) (2,0) (1,1)(3,-1)(-1,3)………
so, it has infinite solutions.
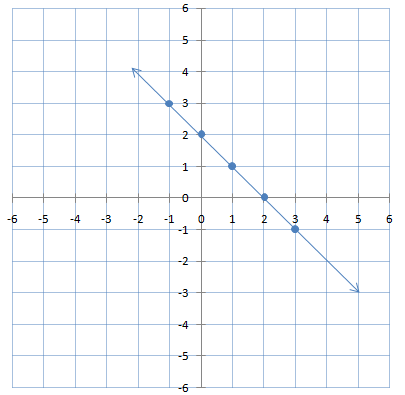

Now let’s plot a graph for these values of x and y.
By plotting and joining these points on the graph we get a straight line. Any point on this straight line satisfies the given equation and point outside the line does not satisfy.
Therefore the geometrical or graphical representation of a degree 1 polynomial is a straight line.
Pair Of Linear Equations In Two Variables
Let’s understand this with an example
Pappulu went to a bookstall to buy pens and books. The number of pens he buys is twice the number of books. The cost of one pen is Rs 5 and for one book it is Rs 20. The total amount he paid to the shopkeeper is Rs 150. Here to find the number of pens and books he bought we form two equations by considering the two situations and solve for.
Here pappulu made two actions
Let’s form equations for these two actions.
Action 1: Buying pens twice that of books
Let the number of pens is ‘x’ and the number of books is ‘y’.
Then, x=2y———–(1)
Action 2: Amount paid by him for one pen and one book is Rs 5 and Rs 10 respectively and the overall amount equals Rs 150.
The amount for ‘x’ pens =5x
The amount for ‘y’ pens =10y
Total amount = 5x+10y——–(2)
Here the equations formed relate to actions of the same person pappulu and these equations are having the same variables ‘x’ & ‘y’. So, these kinds of equations are called a pair of linear equations in two variables.
The general form of a pair of linear equations in two variables ‘x’ and ‘y’ is represented as
\begin{align*}
\begin{aligned}a_{1}x+b_{1}y+c_{1}=0\\ a_{2}x+b_{2}y+c_{2}=0\end{aligned}
\end{align*}
Graphical / Geometrical Representation For Pair Of Linear Equations In Two Variables
There are 3 possible ways for the geometrical representation of a pair of linear equations in two variables. They are
- Two lines intersect at a point
- Two lines parallel to each other. (that is two lines will not intersect each other)
- Two lines will coincide.
Consistency And Inconsistency Of Pair Of Linear Equations In Two Variables
- When a system containing a pair of linear equations in two variables is said to be consistent then, it has at least one solution.
- If a system contains a pair of linear equations in two variables that are said to be inconsistent then it has no solution.
Let’s check conditions for consistency and inconsistency for a pair of linear equations in two variables \begin{align*}
\begin{aligned}a_{1}x+b_{1}y+c_{1}=0\\ a_{2}x+b_{2}y+c_{2}=0\end{aligned}
\end{align*}
| Compare The Ratios | Graphical Representation | Algebraic Interpretation |
|
\begin{align*} |
Intersecting Lines | Exactly One Solution (Unique) |
|
\begin{align*} |
Coinciding Lines | Infinitely Many Solutions |
|
\begin{align*} |
Parallel Lines | No Solution |
All the homogeneous equations which are in the form of ax+by=0 passes through origin. Such system is always said to be consistent.
Quadratic Equations In Algebraic Equations Lists
Any equation which can be represented in the form of ax2+bx+c=0 is called Quadratic equation. Where a≠0.
Quadratic equation has two roots. These roots may be real or complex. Let the two roots be α, β.
Quadratic Equations Can Be Solved In 3 Methods
Factorization Method
In this method, we split the middle term and solve for the roots.
Example:
Let us consider a quadratic equation x2+6x-16=0
x2+8x-2x-16=0
x(x+8)-2(x+8)=0
(x-2)(x+8)=0
x-2=0 ; x+8=0
x=2 ; x=-8
Values of x are 2 and -8.
Computing Squares Method
Here we reduce the equation to a2+2ab+b2 and solve for roots.
We have a2+2ab+b2 = (a+b)2
Example:
For a quadratic equation x2+6x-16=0
x2+6x-16=0
x2+6x=16
Adding ‘9’ on both sides of the equation.
x2+6x+9=16+9
x2+2×3×x+9=25
x2+2×3×x+9=(±5)2
LHS is in the form of a2+2ab+b2 and can be written as (a+b)2
(x+3)2=(±5)2
x+3 =±5
that is x+3=+5 and x+3=-5
x=2, -8
Solutions of equation are 2, -8.
Formula Method
The equation can be directly solved for roots ( α, β)by using formula \begin{align*}
\alpha ,\beta =\dfrac {-b\pm \sqrt {b^{2}-4ac}}{2a} \end{align*}
Example:
consider a quadratic equation x2+6x-16=0
\begin{align*}
\begin{aligned}\alpha , \beta =\dfrac {-6\pm \sqrt {\left( 6\right) ^{2}-\left[ 4\times 1\times \left( -16\right) \right] }}{2\times 1}\\ =-\dfrac {6\pm \sqrt {36+64}}{2}\end{aligned}
\end{align*}\begin{align*}
\begin{aligned}=\dfrac {-6\pm \sqrt {100}}{2}\\ =-\dfrac {6\pm 10}{2}\\ =-\dfrac {16}{2},-\dfrac {4}{2}\\ =-8, 2\\
Roots \ of \ the \ equation \ are \ 2 \ and \ -8\end{aligned}
\end{align*}
Non Linear Equations
An algebraic equation with degree 2 or greater is called non linear equation.
A system of non-linear equations consists of two equations of them at least one equation is not a linear equation.
Example:
x+y=10
y=x2+2
Linear Inequalities In Algebraic Equations List
Here we use certain signs to represent a sentence in the equation.
These signs are called inequalities.
| Symbols of inequality | Read As |
| < | less than |
| > | greater than |
| ≤ | less than or equal |
| ≥ | greter than or equal |
Different types of inequalities with examples
| Type of inequalities | Example representation |
| Numerical inequalities | 9<12, 10>5 |
| Linear inequalities | x<10, y≥5 |
| Double inequalities | 5<x≤10 |
| Strict inequalities | ax+b<0, ax+by≤d, ax+b>0, ax+by≥0 |
| slack inequalities | ax+b≤0, ax+by≤d ax+b≥0, ax+by≥d |
| Linear inequalities in one variable ‘x’ | ax+b<0, ax+by≤0 ax+b>0, ax+by≥0 where a≠0 |
| Linear inequalities in two variables ‘x’ and ‘y’ | ax+by<c, ax+by≤c ax+by>c, ax+by≥c where a≠0 and b≠0 |
| Quadratic inequalities in one variable ‘x’ | ax2+bx+c<0, ax2+bx+c>0 ax2+bx+c≤0, ax2+bx+c≥0 |
When the negative sign is shifted then inequality signals changes.
Example:
-a<b this can also be represented as
a>-b
Read More
| Algebraic Expressions | Algebraic Properties |
| Algebra Multiplication Rules | AP and GP |






