Lines and angles concepts are explained clearly below with all the definitions and properties involved in it. These concepts are useful in clearing many competitive exams like GMAT, CAT, GRE, etc.
Line
A line is formed by joining collinear or non-collinear points.
Types of lines
There are two types of lines
- Straight-line
A line that travels a certain distance without any diversion in a straight path is called a straight line. A straight line has no endpoint.
- Curved line
A line that has diverted paths when traveled is a curved line.
Line segment
The line segment is a line that has two endpoints.
Ray
Ray is a line that has one endpoint. A ray can be extended in only one direction.
Parallel Line
A pair of lines are said to be parallel if they don’t intersect with each other and the distance between those lines is the same.
Parallel lines are denoted by the symbol “||”.
Transversal Line
A line that intersects two or more lines at distinct points is called a transversal line.
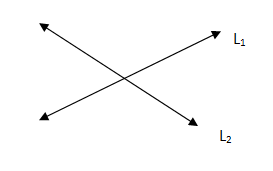
Intersecting Lines
Two lines that intersect each other at a point are called intersecting lines. Intersecting lines share a common point.
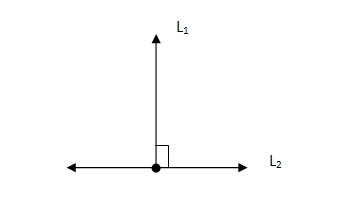
Perpendicular Lines
Two lines are said to be perpendicular lines if they intersect each other at right angles i.e, 90°. Perpendicular lines are denoted by the system “⊥”.
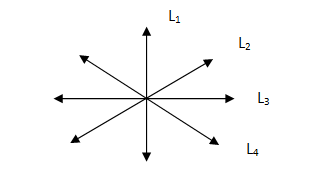
Concurrent Lines
If two or more lines intersect each other at a common point then those lines are said to be concurrent lines.
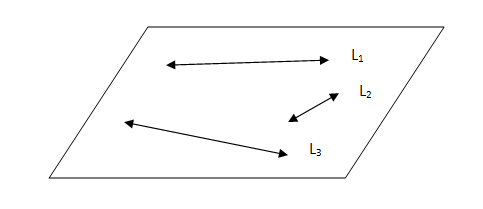
Co-planar Lines
Co-planar lines are those lines which lie in the same planar.
Non-Co-Planar Lines
Non-co-planar lines are those lines which do not lie in the same planar.
Some important points in Lines and Angles
- The infinite number of lines can be drawn through a single point.
- A straight line consists of an infinite number of points on it.
- Two lines can intersect with each other at only one point.
- Two or more points lying on a line are called collinear points.
- Points lying in the same plane are called coplanar points otherwise they are called non-coplanar lines.
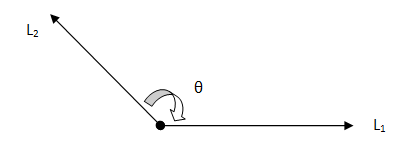
Angles
Two rays starting at a single point form an angle or simply an angle is formed by intersecting two lines.
An angle is represented by the symbol “∠”.
Types of Angles
Acute Angle
An angle that is greater than 0° and less than 90° is called an acute angle.
The acute angle lies between 0° and 90°.
Right Angle
An angle that is exactly equal to 90° is called a right angle.
Obtuse Angle
An angle that is greater than 90° and less than 180° is called an obtuse angle.
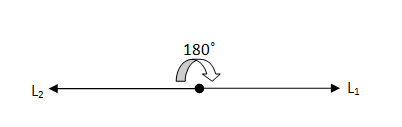
Straight Angle
An angle that is exactly equal to 180° and less than 360° is called a straight angle.
Reflex Angle
An angle that is greater than 180° and less than 360° is called a reflex angle.
Complementary Angle
If the sum of two angles is equal to 90° then those two angles are called complementary angles.
Supplementary Angles
If the sum of two angles is equal to 180° then those angles are called supplementary angles.
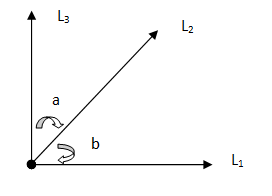
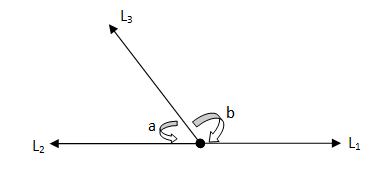
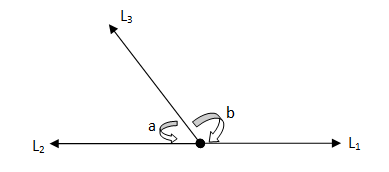
Linear Pair
Two angles are said to be linear if they are adjacent to each other, share a common side and sum of their angles is equal to 180°.
- ∠a and ∠b are adjacent to each other.
- They share a common side l2
- ∠a+∠b=180°.
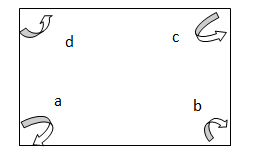
Adjacent Angles
Two angles are said to be adjacent angles if they share a common side.
Here adjacent angles are ∠a and ∠b; ∠b and ∠c; ∠c and ∠d; ∠a and ∠d
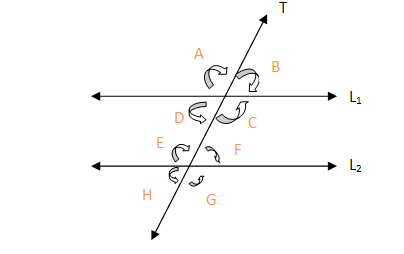
Angles between Parallel Lines
l1 and l2 are parallel lines.
T is a transversal.
Interior Angles
Angles that lie inside parallel lines are interior angles.
∠C,∠D,∠E, and ∠F are interior angles.
Exterior Angles
Angles that lie outside parallel lines are exterior angles.
∠A, ∠B, ∠H, and ∠G are exterior angles.
Interior Alternate Angles or Alternate Interior Angles
Angles that are inside parallel lines and lie on either side of traversal are called interior alternate angles.
∠D and ∠F are interior alternate angles.
∠C and ∠E are interior alternate angles.
Here ∠D=∠F and ∠C=∠E
Exterior Alternate Angles or Alternate Exterior Angles
Angles that are outside parallel lines and lie on either side of traversal are called exterior alternate angles.
∠A and ∠G are exterior alternate angles.
∠B and ∠H are exterior alternate angles.
Here ∠A=∠G
∠B=∠H
Corresponding Angles
∠A = ∠E; ∠B=∠F
∠D=∠H ; ∠C=∠G
Consecutive Interior Angles
∠D and ∠E; ∠C and ∠F are consecutive interior angles.
The sum of consecutive interior angles is 180°.
Here ∠D+∠E=180°
∠C+∠F=180°
Note
Consecutive interior angles are supplementary angles.
Vertically Opposite Angles
The angles which lie vertically opposite to each other when any two lines intersect each other are called vertically opposite angles.
∠A and ∠C, ∠B and ∠D, ∠E and ∠G, ∠H and ∠F are vertically opposite angles.
Note
| Angles in Parallel Lines | Angles |
| Interior angles | ∠C,∠D,∠E, & ∠F |
| Exterior angles | ∠A,∠B,∠H,&∠G |
| Interior alternate angles | ∠D & ∠F, ∠C & ∠E here ∠D=∠F & ∠C=∠E |
| Exterior alternate angles | ∠A & ∠G,∠B & ∠H, ∠A=∠G; ∠B=∠H |
| Corresponding angles | ∠A & ∠E, ∠C & ∠F, ∠D & ∠H, ∠C & ∠G, ∠A=∠E, ∠B=∠F, ∠D=∠H,∠C=∠G |
| Consecutive interior angles | ∠D & ∠E, ∠C & ∠F, ∠D+∠E=180°, ∠C+∠F=180° |
| Vertically opposite angles | ∠A & ∠C, ∠B & ∠D, ∠E & ∠G, ∠H & ∠F |