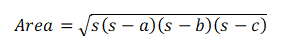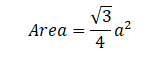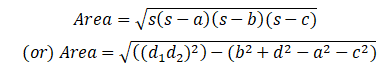Formulas of Mensuration in Maths: Mensuration concept from basics are explained below with important mensuration formulas and properties of geometrical figures.
What is mensuration?
Mensuration is a branch of which, where measurement of various geometrical shapes. The measurements are area, volume, curved surface area, lateral surface area, total surface area, etc.
Types of Geometrical Shapes:
There are two types of geometrical shapes in mensuration. They are
- 2-dimensional
- 3-dimensional
2-Dimensional Geometrical Shape
It is the shape formed by joining three or more straight lines in a plane. 2D geometrical shapes have length and breadth. Here measurements are area, perimeter only.
The units of measurements are
Area: cm², M²,km2, miles².
Perimeter: cm,m,km,miles.
3-Dimensional Geometrical Shape:
It is the shape formed by joining the number of planes or surfaces. 3D- geometric shape has length, breadth, and height(or depth).
Here measurements are volume, curved surface area (CSA), lateral surface area (LSA) and total surface area (TSA).
Some Important Terms in 2D Geometric Shapes
Area
It is the amount of space inside the geometrical figure.
Perimeter
It is the sum of lengths of all sides of a geometrical figure.
Mensuration 2D Formulas in Maths
Triangle
Area of triangle =(1/2)×base×height
⇒(1/2)×b×h
Perimeter = a+b+c
Scalene Triangle
Here, s=a+b+c/2
Perimeter= a+b+c
Isosceles Triangle
Area = ½×b×h (or)
Perimeter= 2a+b
Right Isosceles Triangle
area= (½)× b2 or ¼(hypotenuse)2
Equilateral Triangle
Right Angled Triangle
Area=1/2×b×h
Perimeter=b+h+hypotenuse
Quadrilateral
Here, d1, d2 are diagonal and s= (a+b+c+d)/2
Perimeter=a+b+c+d
Square
Area=s2
⇒ d2/2, here d is diagonal
Perimeter = 4s
Rectangle
Area=l×b
Perimeter= 2×(l+b)
Parallelogram
Area=b×h
Perimeter=2(l+b)
Rhombus
Area=1/2×d1×d2
Perimeter=4a
Trapezium
Area=1/2×(a+b)×h
Perimeter=a+b+c+d
Circle
a = πr2 or πd2/4 d=2r
Here d=diameter and r=radius
Perimeter=2πr (or) πd
Semi Circle
A=Πr2/2 (or) Πd2/8
p=πr + 2r (or) (36/7)r
For Equivalent Triangle having Inside Circle or Inscribed Circle
In-radius of inscribed circle=a/2√3
Area of incircle= (π /12)a2
For Equilateral Triangle thing Circumcircle
circumradius of circum circle=a/√3
Area of circum circle= (π/3)a2
Some important Formulas for Areas of Regular Polygons
| No. of sides | Regular polygon | Area |
| 3 | Equilateral triangle | 0.433 s2 |
| 4 | Square | 1s2 |
| 5 | Pentagon | 1.720s2 |
| 6 | Hexagon | 2.598 s2 |
| 7 | Septagon | 3.6434 s2 |
| 8 | Octagon | 4.828 s2 |
| 9 | Nanogon | 6.182 s2 |
| 10 | Decagon | 7.694 s2 |
Sector of Circle
r=radius
θ=angle in radius
Area of sector=lr/2 (or) (θ/360)×πr2
length of Arc l=θr (or) (θ/360) ×2πr
Ellipse
x=semi major axis
y=semi minor axis a= πxy
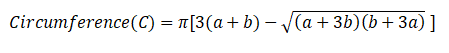
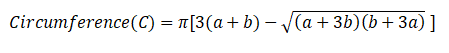
Annulus
r is the inner radius
R is the outer radius
Area A= π(R2-r2)
Width=R-r
Triangle
If r is in the radius of a triangle then
Area= r x s
If R is circumradius of a triangle
Area=abc/4R
Area of triangle=1/2 absinθ
3D units of Measurements are
volume:cm3 (or) m3
LSA: m2 (or) cm2
CSA: m2 (or) cm2
TSA: m2 (or) cm2
Some important Terms in 3D Geometrical Shapes
Volume: It is the total space included inside the 3D shape.
Volume= area of the base x height
LSA (Lateral Surface Area): It is the area of all vertical faces excluding the area of bases of the 3D shape.
Eg: cube, cuboid.
CSA(Curved Surface Area): It is the area of all curved regions of a 3D- shape.
Eg: sphere, cylinder, cone, hemisphere.
TSA(Total Surface Area): It is the sum of areas of all the surfaces of a 3D shape.
Eg: cube, cuboid, cylinder, cone, sphere, hemisphere.
Mensuration 3D Formulas in Maths
Cube
S=side
Volume=s3 cubic units
Total surface area (TSA)= 6s2 sq. Units


Face diagonal= √2×s
Diagonal of cube= √3×s
LSA=4s2
Cuboid/Rectangular Solid
l = length
b= breadth
h= height
Volume= l x bx h
LSA= 2h(l+b)
TSA= 2(lb+bh+lh)
![]()
![]()
Cylinder
r= radius
h=height
volume= πr2h
Curved Surface Area(CSA)= 2πrh
Total Surface Area= 2πr(h+r)
Area of base= area of top= πr2
Sphere
r=radius
volume= (4/3)× πr3
Curved Surface Area of Sphere= Total Surface Area of Sphere= 4πr2
Hemisphere
r=radius
volume=2/3 πr3
Curved surface area= 2πr2
Total surface area of hemisphere= 3πr2
Right Circular Cone
r=radius
h=height
l=slant height
Volume of cone= 3Πr2h
Curved surface area of cone= πrl
Total surface area of cone= πr(r+l)
![]()
![]()
Frustum of a cone
r=top radius
R=base radius
h=height
l=slant height
Volume= (Π/3)(r2 +rR+R2 )h
The curved surface area of a frustum of a cone= πl(r+R)
The total surface area of a frustum of a cone=πl(r+R)πr2+πR2
= πl(r+R)+π(r2+R2)
Slant height of the frustum of cone is ![]()
![]()
Mensuration Formulas for Prism in maths
Prism is a polyhedron that is formed by joining lateral faces of two polygonal bases that are parallel to each other. These lateral faces are perpendicular to their polygonal bases.
Prism Formulas in General
Surface area of a prism= (Lateral Surface Area)+(2 x Base Area)
Lateral surface area = perimeter of base x slant height
Volume= base area x height
Rectangular Prism
Volume of rectangular prism= l×b×h
Total surface area of rectangular prism=2(l×b+b×h+l×h)
Triangular Prism
Base area=12ab
olVume= ½ abh
TSA= ab+3bh
Here a= apothem length; b= base ; h=height
Prism example problem with a solution
Question: The base of a right prism is a triangle and the lengths of its sides are 15cm, 25cm and 30 cm. The height of the prism is 10 cm. Find the volume, lateral surface area, and total surface area of prism?
Solution:
Let ‘s’ be the semi-perimeter of the base of the prism s=(15+25+30)/2 = 35 cm
Volume of the prism=(area of base) x height
=187 x 10
=1870 cu. Cm
The lateral surface area of prism= (perimeter of base x slant height)
perimeter of base=(15+25+30)=70
LSA=(70 x 10)= 700
TSA of triangular prism=( LSA + 2 × base area)
=(700 + 2 × 187)
=1074 cu. cm
Mensuration Formulas for a pyramid
The pyramid is a polyhedron where lateral faces are triangular formed by connecting a polygonal base and a point called the apex.
A pyramid with n sided base has
- Verticles (n+1)
- Faces (n+1)
- Edges 2n
Pyramid Formulas in General
Volume=(1/3) × (base area) x height
Lateral surface area= ½ (perimeter of base) x lateral height
lateral height =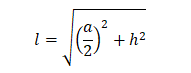
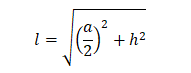
a=base of square/rectangle/triangle
h=height
Total surface area of pyramid= lateral surface area+area of base
Square Pyramid
a=side
s=slant height
h=height
Volume = (¹⁄3)×a²×h
Total surface area= 2as+a2
Triangular Pyramid
a=base length
b=apothem length
s=slant height
h=height
Volume of triangular pyramid=(¹⁄6 )×a×b×h
Total surface area of triangular pyramid= ½ ab + 3/2 as
Regular Tetrahedron
a=side
Volume= (1/12)×(√2a³)
Total surface area=√3a²