What are The Factors of 75

When dealing with factors of a number to be found, the question of what the factors of 75 are arises. Numerous techniques, including multiplication, division, and prime factorization, can be used to accomplish this.

What are the Factors of 75

The numbers that divide 75 perfectly while leaving no remainder are known as factors of 75. In plain English, it can be said that two numbers are factors of 75 if their product, when multiplied, is 75.

Factors of 75 are: 1, 3, 5, 15, 25 and 75.

Let’s pick a number called 3 from above

1. 75 ÷ 3 = 25
2. Here quotient = 25 and remainder = 0
3. If we multiply 25 and 3 product is 25 × 3 = 75
4. Therefore, 25 and 3 are factors of 75

How to find factors of 75 using different methods 

There are different methods to find factors of a number. By applying any of these methods it can easy to find the factors of 75

How to find factors of 75 by multiplication method 

In the multiplication method, we consider the numbers that when multiplied in pairs result to 75

Let’s see the multiplication process

1 × 75 = 75
3 × 25 = 75
5 × 15 = 75
15 × 5 = 75
25 × 3 = 75
75 × 1 =75 (Product repeats in reverse order multiplication )

So the factors of 75 are 1, 3, 5, 15, 25, and 75.

How to find factors of 75 by division method

In the division method, we consider the numbers which exactly divide 75 with leaving a remainder.

Let’s see the division process

75 ÷ 3 = 25
75÷ 5 = 15
75 ÷ 15 = 5
75 ÷ 25 = 3

As 1 and itself are factors of any number 1 and 75 are also factors of 75.
There all the numbers 1, 3, 5, 15, 25, and 75 are factors of the number 75.

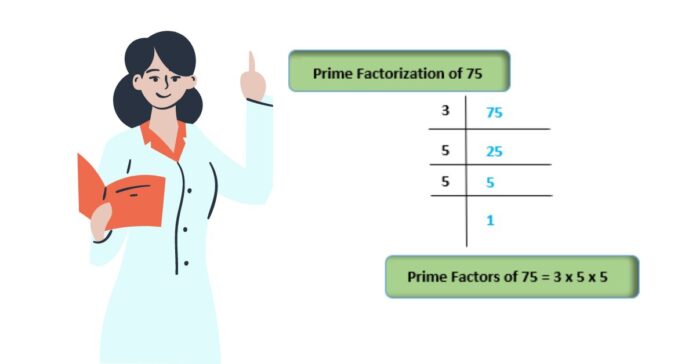
How to find factors of 75 by prime factorization method 

In the prime factorization method, we consider the numbers written as a product of prime factors as prime factors of 75. 

The following steps help in finding the prime factors of a number

Step 1: Divide the given number 75 by the least prime number (3).
75 ÷ 3 = 25

Step 2: If the resultant number is not divisible by this number (3) then, divide it using the next least prime number(5).
25 ÷ 5 = 5

Step 3: As the resultant number 5 is divisible by 5 we divide it by 5.
5 ÷ 5 = 1

Considering all the above steps the prime factors of 75 are 3 × 5 × 5 => 3 × 5².

The prime factors of 75 are 3 × 5 × 5 => 3 × 5².

Factors of 75 in pairs and product form

According to the information shown above, if the product of two numbers is equal to 75, then those numbers are factors of 75. There may be negative aspects to the number 75 because the sum of two negative numbers is positive. Consequently, we have a pair of positive factors of 75 and a negative pair of factors of 75.  

Positive pair of factors of 75

Positive Factors of 75	Positive pair of factors of 75
1 × 75	(1, 75)
3 × 25	(3, 25)
5 × 15	(5, 15)
15 × 5	(15, 5)
25 × 3	(25, 3)

Here (3, 25) is the same as (25, 3), and (5, 15) is the same as (15, 5).
Therefore the positive factors of 75 are (1, 75), (3, 25), and (5, 15).

Negative pair of factors of 75

Positive Factors of 75	Positive pair of factors of 75
-1 × -75	(-1, -75)
-3 × -25	(-3, -25)
-5 × -15	(-5, -15)
-15 × -5	(-15, -5)
-25 × -3	(-25, -3)

Here (-3, -25) is the same as (-25, -3), and (-5, -15) is the same as (-15, -5).
Therefore the positive factors of 75 are (-1, -75), (-3, -25), and (-5, -15).

Factors of 75 solved example problems

Example 1: How are the factors of 75 and 36 related?

Solution: 

        Factors of 75 are 1, 3, 5, 15, 25, and 75.
        Factors of 36 are 1, 2, 3, 4, 6, 9, 12 and 36.
Factors of 75 and 36 are related by common factors and all the factors of 75 are included in 36.
The common factors of 75 and 36 are 1 and 3.

Example 2: Can you list the factors of 75 and its factor pair?

Solution: 

             The list of factors of 75 is 1, 3, 5, 15, 25, and 75.
            The list of factor pairs of 75 is
Positive factor pair of 75: (1, 75), (3, 25), and (5, 15).
Negative factor pair of 75: (-1,- 75), (-3,- 25), and (-5, -15).

Example 3: Find the average sum of all the prime factors of 75?

Solution: 

             Prime factors of 75 are 3 and 5
The average sum of prime factors of 75 is 3+5 = 8

Example 4: Find the product of all the prime numbers of 75?

Solution: 

             Prime factors of 75 are 3 and 5.
The product of all the prime numbers of 75 is 3 × 5 = 15

Example 5: Find the common factors of 75 and 150?

Solution: 

             The Factors of 75 are 1, 3, 5, 15, 25 and 75.
            The factors of 150 are 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, and 150.
The common factors of 75 and 150 are 1, 3, 5, 15, 25 and 75.

FAQ’ s

1. What are the prime factors of 75?
   Ans: The prime factors of 75 are 3 and 5.
2. How many factors does 75 have?
   Ans: The number of factors of 75 has are 6. 
3. What are the common factors of 75?
   Ans: The common factors of 75 are positive factors of 75 and negative factors of 75. Positive factors of 75 are 1, 3, 5, 15, 25, and 75.
   Negative factors of 75 are -1, -3, -5, -15, -25, and -75.
4. What numbers are the factors of 75?
   Ans: The numbers of factors of 75 are 1, 3, 5, 15, 25, and 75.
5. What are the factors of 75 and 90?
   Ans: The factors of 75 are 1, 3, 5, 15, 25, and 75.
   Factors of 90 are 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, and 90.
6. What are the factors of 75 in pairs?
   Ans: Factors of 75 in pairs are (1, 75), (3, 25), and (5, 15).
7. What are the common factors of 75 and 100?
   Ans: Factors of 75 are 1, 3, 5, 15, 25, and 75.
   Factors of 100 are 1, 2, 4, 5, 10, 20, 25, 50, and 100.
   The common factors of 75 and 100 are 1, 3, 5, and 25.
8. What are the common factors of 75 and 60?
   Ans: Factors of 75 are 1, 3, 5, 15, 25, and 75.
   Factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60.
   The common factors of 75 and 60 are 1,3, 5, and 15.
9. What are the common factors of 75 and 30?
   Ans: Factors of 75 are 1, 3, 5, 15, 25, and 75.
   Factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30.
   The common factors of 75 and 30 are 1, 3, 5, and 15.